Object API

Object API#

In TomoPhantom, we have a dedicated functionality that allows the user to build bespoke phantoms by stacking multiple objects together. One should look into the Object() function of tomophantom.TomoP2D() or tomophantom.TomoP3D() modules if one wishes to build a 2D or 3D phantom, respectively. If one needs also projection data to be generated, then please see the ObjectSino() function in the same modules.

One can notice that one of the input parameters for Object() and ObjectSino() functions is obj_params (a dictionary or a list of dictionaries with the parameters for object(s)). The Parameters of 2D objects explained section gives the details about the meaning of parameters for 2D objects and Defining 2D objects in Python explains how to use it in Python. For 3D phantoms, see also Parameters of 3D objects explained and Defining 3D objects in Python sections, respectively.

Parameters of 2D objects explained#

There are 7 parameters in total to describe a 2D object. Please refer to Fig. 1 when exploring parameters bellow.

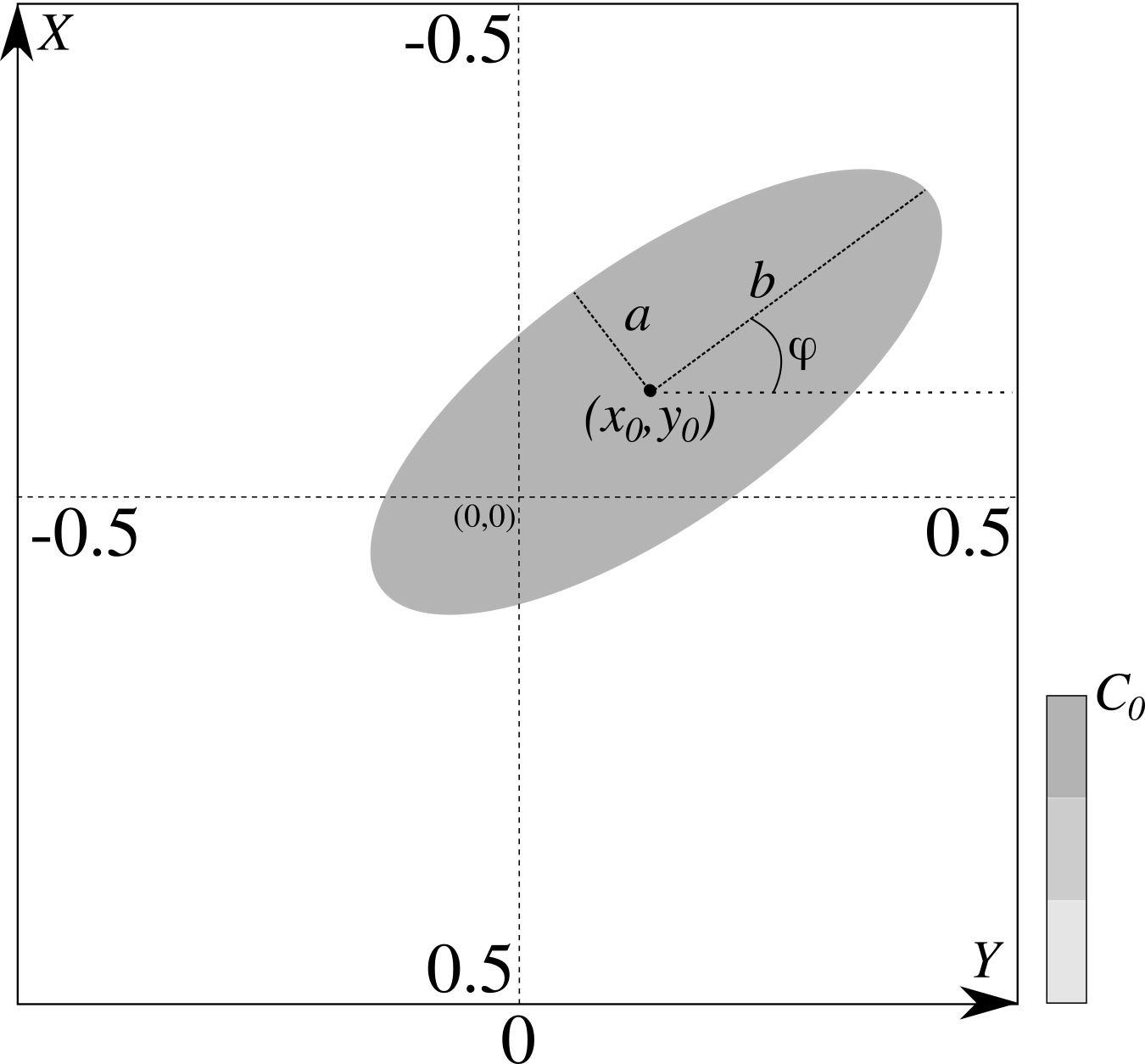
Notation for a 2D object — Fig. 1 The coordinate system in which the objects are defined and an ellipsoid object as an example. Note the position of \(X\) and \(Y\) axes and the ranges for the visible field of view. Parameters describing a 2D object are: object’s name, \(C_{0}\), \(x_{0}\), \(y_{0}\), \(a\), \(b\) and the rotation angle \(\phi\), see detailed description above.#

Parameters of 2D objects in library file#

More general information about what the library file can contain is given in Library files API. Here we look at the part where the object is described:

Object : ellipse 1.0 0.0 0.0 0.69 0.92 0.0;

TomoPhantom converts this string for a 2D model into the following behind the scenes:

objects_name="ellipse" # object's name
C0=1.0 # object's intensity level
x0=0.0 # object's center along the X-axis
y0=0.0 # object's center along the Y-axis
a=0.69 # object's half-width
b=0.92 # object's half-length
phi=0.0 # object's rotation angle

Defining 2D objects in Python#

In order to create a 2D object in Python one should use Object() function of tomophantom.TomoP2D() to create a phantom-object and ObjectSino() function to generate sinogram data for that object.

You will need to create a dictionary for one object or a list of dictionaries for multiple objects. For example, to create a phantom with one object one can do:

from tomophantom import TomoP2D
from tomophantom.TomoP2D import Objects2D
phantom_size = 256
object1 = {
    "Obj": Objects2D.GAUSSIAN,
    "C0": 1.00,
    "x0": 0.25,
    "y0": -0.3,
    "a": 0.15,
    "b": 0.3,
    "phi": -30.0,
}
phantom = TomoP2D.Object(phantom_size, object1) # which will generate 256^2 phantom

Note

To define object’s name in the enum class Objects2D one need to use capital letters for objects: GAUSSIAN, PARABOLA, PARABOLA1, ELLIPSE, CONE, RECTANGLE.

And for multiple objects stacked together, one can do

from tomophantom import TomoP2D
from tomophantom.TomoP2D import Objects2D
phantom_size = 256
object1 = {
    "Obj": Objects2D.GAUSSIAN,
    "C0": 1.00,
    "x0": 0.25,
    "y0": -0.3,
    "a": 0.15,
    "b": 0.3,
    "phi": -30.0,
}
object2 = {
    "Obj": Objects2D.RECTANGLE,
    "C0": 1.00,
    "x0": -0.2,
    "y0": 0.2,
    "a": 0.25,
    "b": 0.4,
    "phi": 60.0,
}
myObjects = [object1, object2]  # dictionary of objects
phantom = TomoP2D.Object(phantom_size, myObjects) # which will generate 256^2 phantom

Parameters of 3D objects explained#

3D object is an extension of a 2D object to a third dimension. Most of the parameters remain as in Parameters of 2D objects explained, but we will list them bellow for clarity as we have now 11 parameters in total:

Warning

The phantom objects can be controlled using all three Euler angles \(\phi_{1-3}\). However, if one also would like to generate projection data analytically, please use \(\phi_{2-3} = 0\). The full support of all three angles is not working currently, you still can use \(\phi_{1}\) for both phantom and data generation.

Parameters of 3D objects in library file#

More general information about what the library file can contain is given in Library files API. Here we look at the part where the object is described:

Object : ellipsoid 1.0 0.0 0.0 0.0 0.69 0.92 0.81 0.0 0.0 0.0

TomoPhantom converts this string for a 3D model into the following behind the scenes:

objects_name="ellipsoid" # object's name
C0=1.0 # object's intensity level
x0=0.0 # object's center along the X-axis
y0=0.0 # object's center along the Y-axis
z0=0.0 # object's center along the Z-axis
a=0.69 # object's half-width
b=0.92 # object's half-length
c=0.81 # object's half-depth
phi1=0.0 # object's rotation angle
phi2=0.0 # object's rotation angle
phi3=0.0 # object's rotation angle

Defining 3D objects in Python#

In order to create a 3D object in Python one should use Object() function of tomophantom.TomoP3D() to create a phantom-object and ObjectSino() function to generate projection data for that object.

You will need to create a dictionary for one object or a list of dictionaries for multiple objects. For example, to create a phantom with one object one can do:

from tomophantom import TomoP3D
from tomophantom.TomoP3D import Objects3D
phantom_size = 256
object1 = {
    "Obj": Objects3D.GAUSSIAN,
    "C0": 1.0,
    "x0": -0.25,
    "y0": -0.15,
    "z0": 0.0,
    "a": 0.3,
    "b": 0.2,
    "c": 0.3,
    "phi1": 35.0, # note that phi2,3 are not set here. They are equal to zero by default.
}
phantom = TomoP3D.Object(phantom_size, object1) # which will generate 256^3 phantom

Note

To define object’s name in the enum class Objects3D one need to use capital letters for objects: GAUSSIAN, PARABOLOID, ELLIPSOID, CONE, CUBOID, ELLIPCYLINDER.

And for multiple 3D objects stacked together, one can do

from tomophantom import TomoP3D
from tomophantom.TomoP3D import Objects3D
phantom_size = 256
object1 = {
    "Obj": Objects3D.GAUSSIAN,
    "C0": 1.0,
    "x0": -0.25,
    "y0": -0.15,
    "z0": 0.0,
    "a": 0.3,
    "b": 0.2,
    "c": 0.3,
    "phi1": 35.0,
}

object2 = {
    "Obj": Objects3D.CUBOID,
    "C0": 1.00,
    "x0": 0.1,
    "y0": 0.2,
    "z0": 0.0,
    "a": 0.15,
    "b": 0.35,
    "c": 0.6,
    "phi1": -60.0,
}
myObjects = [object1, object2]  # dictionary of objects
phantom = TomoP3D.Object(phantom_size, myObjects) # which will generate 256^3 phantom