Model 2D and reconstruction

Using TomoPhantom to:

• build a phantom from the existing library of phantoms

• generate analytical sinogram from it and add noise to it

• reconstruct the noisy sinogram using the Fourier method (ToMoBAR package required).

import numpy as np
import matplotlib.pyplot as plt
from tomophantom import TomoP2D
import os
import tomophantom
from tomophantom.qualitymetrics import QualityTools

plt.rcParams['figure.figsize'] = [12, 8]
plt.rcParams['figure.dpi'] = 80

# generate a phantom
model = 4 # select a model
N_size = 512 # set the dimension of the phantom
path = os.path.dirname(tomophantom.__file__)
path_library2D = os.path.join(path, "phantomlib", "Phantom2DLibrary.dat")
phantom_2D = TomoP2D.Model(model, N_size, path_library2D)

plt.figure(1)
plt.rcParams.update({'font.size': 21})
plt.imshow(phantom_2D, vmin=0, vmax=1, cmap="gray")
plt.colorbar(ticks=[0, 0.5, 1], orientation='vertical')
plt.title('{}''{}'.format('2D Phantom using model no.',model))

Text(0.5, 1.0, '2D Phantom using model no.4')

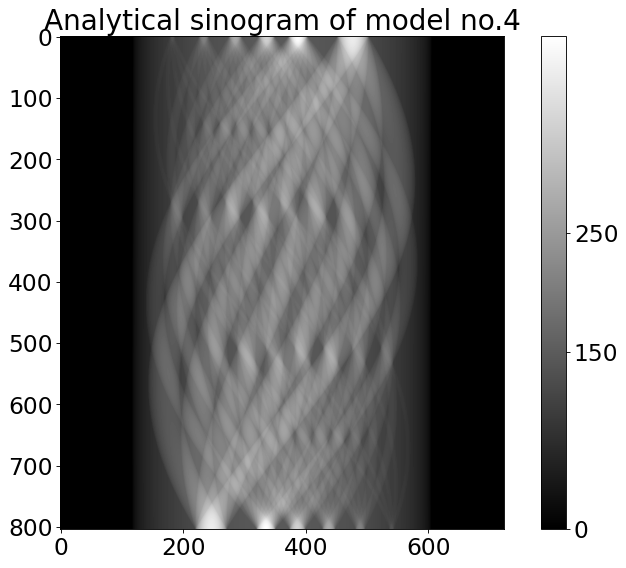
# generate analytical sinogram
angles_num = int(0.5*np.pi*N_size); # angles number
angles = np.linspace(0.0,179.9,angles_num,dtype='float32')
angles_rad = angles*(np.pi/180.0)
P = int(np.sqrt(2)*N_size) #detectors

sino_an = TomoP2D.ModelSino(model, N_size, P, angles, path_library2D)

plt.figure(2)
plt.rcParams.update({'font.size': 21})
plt.imshow(sino_an,  cmap="gray")
plt.colorbar(ticks=[0, 150, 250], orientation='vertical')
plt.title('{}''{}'.format('Analytical sinogram of model no.',model))

Text(0.5, 1.0, 'Analytical sinogram of model no.4')

# Adding some noise to data
from tomophantom.artefacts import artefacts_mix

_noise_ =  {'noise_type' : 'Poisson',
            'noise_sigma' : 10000, # noise amplitude
            'noise_seed' : 0}

noisy_sino = artefacts_mix(sino_an, **_noise_)

plt.figure()
plt.rcParams.update({'font.size': 21})
plt.imshow(noisy_sino,cmap="gray")
plt.colorbar(ticks=[0, 150, 250], orientation='vertical')
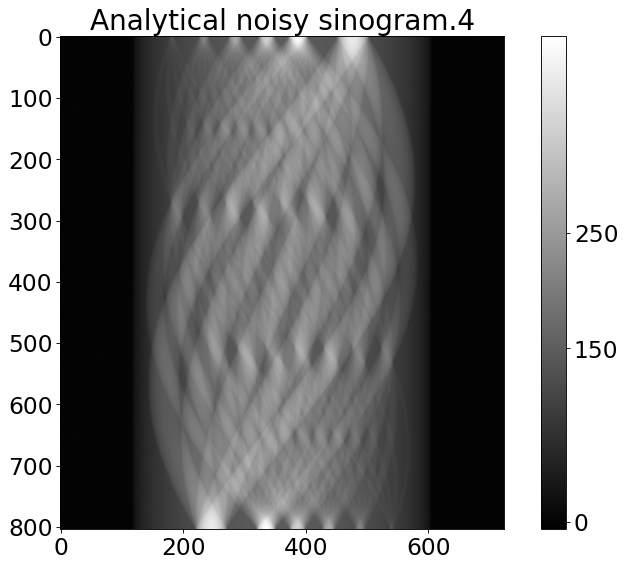
plt.title('{}''{}'.format('Analytical noisy sinogram.',model))

Poisson noise has been added to the data.

Text(0.5, 1.0, 'Analytical noisy sinogram.4')

# one can use a ToMoBAR package to reconstruct the data
# install it with: conda install httomo::tomobar

# initialise tomobar DIRECT reconstruction class ONCE
from tomobar.methodsDIR import RecToolsDIR

RectoolsDIR = RecToolsDIR(DetectorsDimH = P,  # DetectorsDimH # detector dimension (horizontal)
                    DetectorsDimV = None,  # DetectorsDimV # detector dimension (vertical)
                    CenterRotOffset = None, # Centre of Rotation (CoR) scalar
                    AnglesVec = angles_rad, # array of angles in radians
                    ObjSize = N_size, # a scalar to define reconstructed object dimensions
                    device_projector='cpu')
print ("%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
print ("Reconstructing analytical sinogram using Fourier Slice method")
print ("%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%")
RecFourier = RectoolsDIR.FOURIER(noisy_sino, method='linear')
plt.figure()
plt.imshow(RecFourier, vmin=0, vmax=1, cmap="gray")
plt.colorbar(ticks=[0, 0.5, 1], orientation='vertical')
plt.title('Fourier slice reconstruction')

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
Reconstructing analytical sinogram using Fourier Slice method
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%

Text(0.5, 1.0, 'Fourier slice reconstruction')